• 作者: ［英］约翰.黑格
• 出版社: 东方出版中心
• 出品方: 读客文化
• 译者: 徐大成
• 出版年: 2021-3
• 页数: 224
• 定价: 32
• 丛书: 牛津通识课
• ISBN: 9787547317440
• Kindle 每日特价：3.99

01 基本原理 Fundamentals

概率是不确定性这一概念的形式化表述。

古典概率

只是对结果进行计数，并赋予它们相等的概率，

每一个结果都倾向于表现出某个特定的频率，频率论者(frequentist) 认为这个频率值就是相应结果的概率。

主观概率

有至少三个一般性评估主观概率的不同方法。

p 就是你认为这个陈述或者事件的可信度。

古典概型、频率诠释还是可信度，赔率(odds) 这个词语在描述概率的时候经常出现。

02 概率的运作 The Workings of Probability

加法定理

当两个事件互斥时，至少一个事件发生的概率是两个事件各自发生概率的和。

乘法定理

在给定第一个事件发生的条件下，另一个事件的条件概率(conditional probability) 就是它的正常的概率。如果这成立，这两个事件被称为是独立的(independent)，两个事件同时发生的概率就是两个事件单独发生的概率的乘积。

独立性

就应该将整个过程分成若干阶段。找到一个事件的概率；然后，假设这个事件真的发生，再找到第二个事件的概率；再假设前两者均发生，找到第三个事件的概率；然后假设前三者均发生，找到第四个事件的概率——以此类推。最终，将所有的数据相乘。

将独立当作互斥是常见的错误，反之亦然。

加法定理用来计算至少一个事件发生的概率，乘法定理用来推导它们全部发生的概率。

有时人们说：计数真的只有 1、 2、无穷大。这个说法揭示了一条真理，如果我们可以完成从处理一件事到处理两件事的过渡，那随后到第 3、 4、 5 等的过渡相比而言就不那么重要了。

大多数具有“计算这些事件中至少一个发生的概率”这种格式的问题，都可以用这种方式解决：计算它们均不发生的概率，然后从单位 1 中减掉这个概率。

03 历史概要 Historical Sketch

伯努利试验

大数定律

他意识到数字 6 的实际数量与期待的平均数量之间的偏差，可以用投掷次数的算术平方根来进行最适当的描述。

现在通常称之为正态分布(normal distribution)。

逆概率

贝叶斯法则(Bayes’ Rule)。

贝叶斯展示的洞察力在很多年中被忽略了，但是他的确指出了中心问题：如果在一系列的伯努利试验(例如掷色子) 中，成功的概率是未知的，但是试验和成功的次数都分别是已知的，这个不可知的概率落在指定区间内的可能性有多大？而另一位极其优秀的数学家拉普拉斯的计算优于贝叶斯。

中心极限定理

该定理说明了在很多情况下，大量随机数据的和是棣莫弗的正态分布的理想近似状态。我们不需要某个单独数据如何变化的细节，整体数据变化的模式会紧密地贴合这个正态法则。

为了利用这个想法，我们只需要两个数字：第一个是全体数据的平均值，第二个是一个简单地表示它的变化程度的数据。知道这两个数据，任何一个概率都能够从棣莫弗的表格中找到。

高斯分布

观测中的误差真的遵循这个规律吗？亨利·庞加莱(Henri Poincar é)——对数学各分支具有全面知识的最后一位数学家——说：“人人都相信它，因为数学家误以为这是观测中的事实，而观测者认为这是个数学原理。”

泊松分布(Poisson Distribution) 就经常出现在我们计算事件“随机”发生概率的时候，

所有这些例子都符合一个相同的模式：大量的机会，每个机会中事件发生的概率很小。每当你正在研究的现象符合这种模式，泊松分布就很可能对它有用。

如果知道序列中的前一个值，要预测随机变化序列的下一个值的时候，我们都可以忽略更前面的那些值，那么这个序列被称为具有马尔可夫性质(Markov property)。

任意给定公差带，一定会有一个时刻(我们不知道什么时刻，但是的确有那么一个时刻)，在这个时刻之后，实际事件发生的频率就会永久地停留在公差带内部。这被称为强大数定律

测度论

乔·杜布(Joe Doob) 使用术语“鞅”(martingale，这个词原本指每次损失后将赌金加倍的投注策略) 来描述那些在未来某时刻的平均值与现在的值(大致上) 相等的随机量。

04 概率试验 Chance Experiments

离散分布

均匀分布

二项分布

使用二项分布需要 3 个条件：固定试验次数，每个事件与其他事件相互独立，并且事件发生的概率是常数。

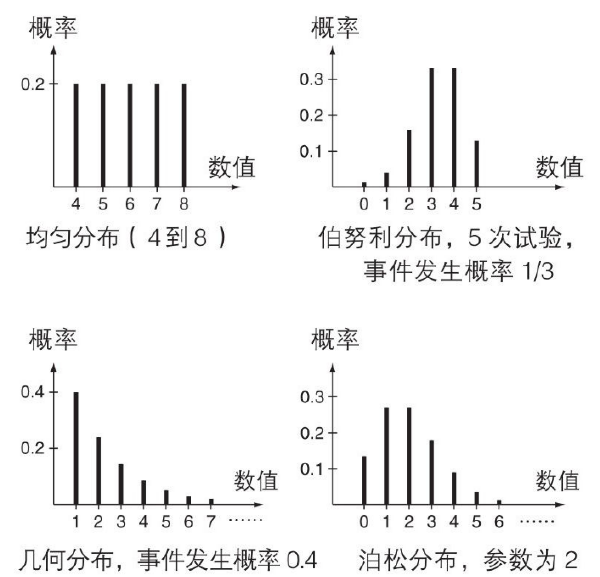
图 4 　一些常见的离散分布

连续分布

概率密度

为了限定一个概率密度，一条曲线一定必须具有两个特性：不能取负值，在曲线下的全部面积必须是单位 1。

指数分布

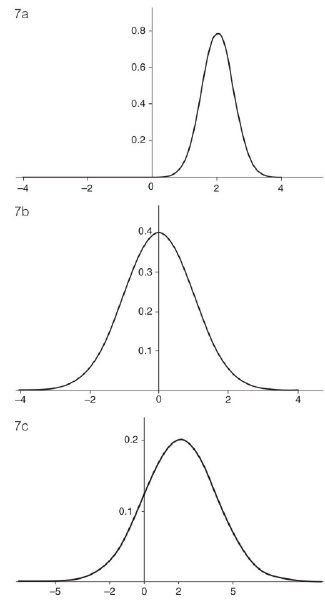
图 7 　高斯分布

我们不再能够认为“不会发生”与“概率为 0”具有相同的意义。

在提前指定的情况下，认为任何概率为 0 的事件都不会发生是合理的。

加权和

等待一个事件发生所需的平均时间是事件发生的概率的倒数。

方差

标准差

极端值分布

在很大的年代跨度中，最大索赔额一共只有三个可能的种类，它们被称为极端值分布，具体的名字是弗雷歇(Fr é chet)、冈贝尔(Gumbel)、韦布尔(Weibull)。

05 理解概率 Maki ng Sense of Probabi l ities

热门冷门偏差

组合小概率

一些误解

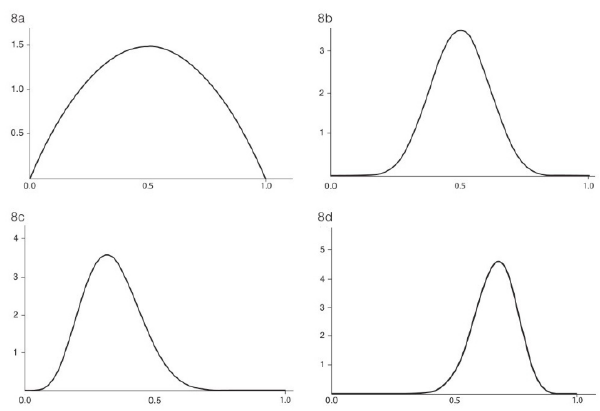
图 8 　贝塔分布的一组图像

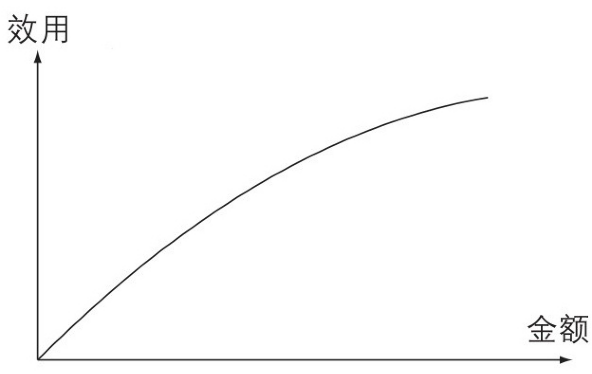
图 9 　一般的效用曲线的形状

06 人们玩的游戏 Games People Play

对于英国的 6/ 49 类型的彩票来说，下面的过程会帮到你。

先验赔率

似然比

后验赔率

后验赔率=先验赔率×似然比

07 在科学、医学和运筹学中的应用 Appl ications in Science, Medici ne, and Operations Research

加法和乘法定理、独立性、将客观概率和频率联系起来的大数定律、在将随机数求和时候使用的高斯分布、其他的一些经常出现的分布函数、反映总体情况时有用的平均值和方差。

就像统计学家乔治·博克斯(George Box) 所说的那样，“所有的模型都不是完全正确的，但是有一些是很有用的”。

布朗运动和随机游走

蒙特卡罗模拟

08 其他应用 Other Appl ications

检察官谬误

通过考虑到贝叶斯公式计算证据有效性的方法，可以避免第二个错误。

随机化回答

当这些事件的真实概率被严重低估的时候，模型就是无效的，而模型导出的结论就根本没有合理的基础。在第 4 章 中提到过的极端值分布可以用来解决这个问题。

相关性

其中有一个无法避免的逻辑陷阱：如果 X 与 Y 负相关， Y 与 Z 负相关，那么 X 与 Z 就似乎是正相关了!

所罗门·博纳(Salomon Bochner) 的数学工作结果证明了在很大的投资组合中，每一对投资都是负相关的确是有可能的。

09 有趣而棘手的问题 Curiosities and Di lemmas

概率这门学科已经完全不含有真实的悖论了。

帕隆多悖论

在所有赌局都对一方有利的时候，无论何种情况我们都不可能找到一种组合让另一方有优势。

彭尼赌局游戏(Penney-ante) 就是基于上述的观点。你请你的对手选择 8 个可能的长度为 3 的一组结果中的任何一个，比如 HHT，或者 THT 等，它们都可能会是连续 3 次投掷公正硬币的结果。之后你选择一个不同的结果，一个中立的人重复投掷硬币，选择了首先出现的结果的那个人获胜。

辛普森悖论

决策论的核心信条：合理的决定是能最大化结果的平均效用。

附录 书中提出的问题的答案

所以 x = 2 + (x / 2)，即 x = 6。

在彭尼赌局游戏中，如果你的对手选择了 HHH，你应该选择 THH，而你获胜的概率是 7/ 8；如果她选择了 HHT，你再一次地选择 THH，获胜可能性为 3/ 4；如果她选择 HTH，你选 HHT，如果她选择 THH，你选 TTH——在这两种情况中，你有 2/ 3 的可能性获胜。利用对称性就可以得到应对 TTT、 TTH、 THT 和 HTT 的最佳选择。